【基礎編】わかりやすい分数の教え方のポイント

知育玩具などを通じて、小さい時からおなじみのお子様も多い分数ですが、基礎を理解していないと、あとで躓いてしまいます。

ここでは分数の教え方のポイントをお伝えします。

分数の意味をきっちり理解する

分数の教えるにあたって、一番大事なのは…

そもそも分数ってなんぞや？

をちゃんと理解することです。

分数のたし算で、仮分数から帯分数に直したり、逆に帯分数から仮分数に直したりする変換も、分母どうしをそのまま足しちゃったらいけない理由も、「分数とは」を理解していればスムーズです。

教える時のポイントは…

お母さんが、ピザを、切っているところをイメージすることです。

分母、分子というワードは、おんぶや肩車している「母」と「子」だと伝えたら、お子様も間違えずに上、下を覚えられるはずです。

そして、分母であるお母さんが、ピザを何等分かに分けるイメージを持たせます。

ここで重要なのは、この分母自体は、個数ではなく、「〇個分に分ける」という「分割量」であるということです。

また、注意したいのは…分けるといっても「等しく分ける」、「等分」するということ。

こんな悪いお母さんいないですよね…？

次に、いくらお母さんが等分したからといって、もともと大きさ同じでなければなりません。

分数が整数になるロジックはピザで考える

1枚のピザを6等分した1ピースは６分の１、２ピースは６分の２、３ピースは６分の３…これを続けていくと…

1枚のピザを6等分した６ピースは…６分の６、出来上がった形を見ると、ピザ丸１枚になりますね！

つまり、分母と分子の数が同じ時は、１になります。

ここで、お母さんがこのように言います。

分数は、一つのものを分母の数分に分けた数を示すので、別に「１以上」になってもいいわけです。

…お子様の頭の中で、分数は「１」より小さいと思っているのであれば、ここで払拭してあげて下さいね。

先ほど同様に、1枚のピザを6等分したピースの数を増やしていってみましょう！

12 ピース分は…２枚になりますね！

つまり…分子が分母で割り切れる時は整数になるということです。

<【がんプリ】分数の基礎

ここまでのプリントを以下にまとめました。

仮分数・帯分数は、ピースで考えるか丸のピザにするかの違い

まずは、大人も忘れていたこのワードの復習

真分数…分子が分母より小さい分数

仮分数…分子と分母が同じか、分子が分母より大きい分数

帯分数…整数と真分数の和で表されている分数

今後、仮分数を帯分数に変換したり、逆に帯分数を仮分数に変換したりする計算が沢山出てくるわけですが、そもそも何が違うの？ということですが…

仮分数はピースで考える、帯分数は1枚のピザに出来るものはしてしまう　というイメージで進めます。

また、ここからは、仮分数や帯分数への変換についてやっていきますが、これらは全て、数量の話、つまり、〇個に分けたものが「いくつあるか」についての計算です。

分母である分割量の話ではありません。よって、分子の計算がメインになります。

その点も、親御さんが意識した上で、教えてあげるようにしましょう。

帯分数を仮分数に直す方法

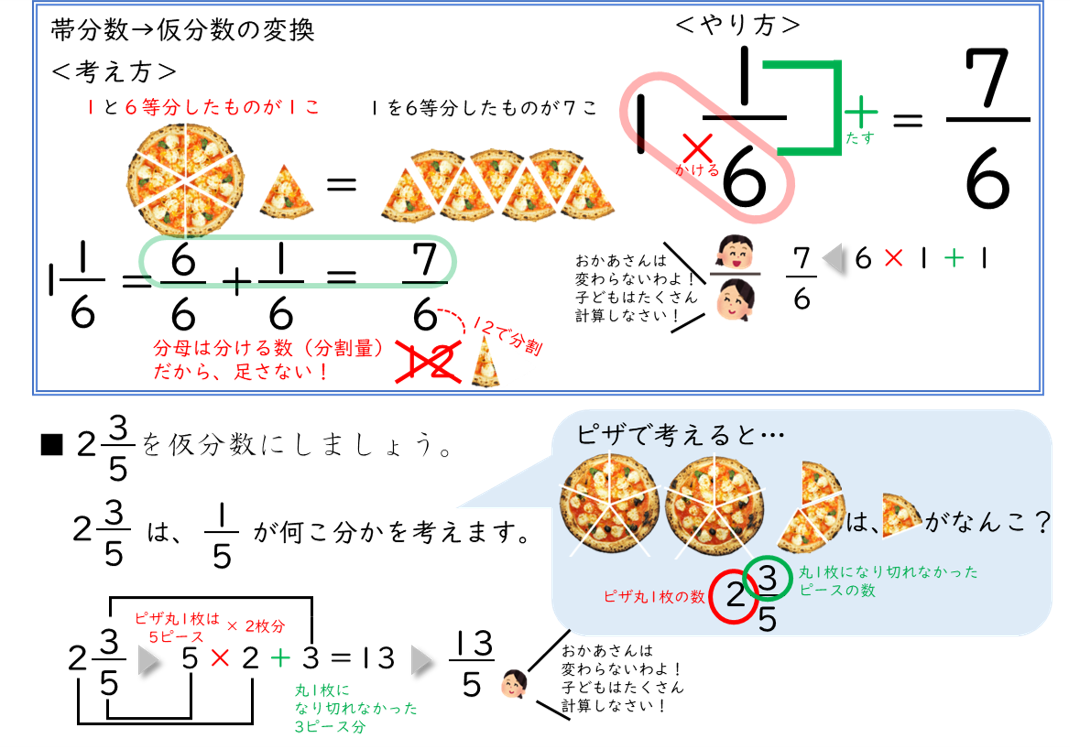
帯分数から仮分数への変換、つまり、丸ピザ（ピースが全部集まり1枚になったピザをこう呼ぶとします）から、ピースに変換するやり方です。

まずは、考え方を理解しましょう。

と、スムーズに出来たらいいですね…！分からなくても、最終的に式の意味が理解出来たら◎！！

また、先ほど、仮分数や帯分数への変換は、数量の話で、分子の計算がメインになるとお伝えしました。

よって、イラストのお母さんも「お母さんは変わらないわよ!子どもは沢山計算しなさい！」と言っているのにも注目です。
…こういうひとつ一つのイメージが、分数を学ぶ上でも大事になってくると思います。

仮分数を帯分数に直す方法

仮分数から帯分数への変換、つまり、沢山のピースがある中で、丸ピザは何枚出来て、何ピースあまるか？を考えます。

【がんプリ】仮分数・帯分数の変換

分数は日常生活にも沢山！日頃から意識することが大事

3人家族なら3等分、4人家族なら４等分…等分する機会は沢山あると思います。

その時に、是非、分数を意識した声かけをしてみてください。